Pi-sica en Movimiento

Por siglos, π fue un número que solo vivía dentro de los círculos. Sin embargo, hoy en día es posible calcular pi con choques elásticos, un método sorprendente que aparece donde menos se espera: en un experimento con colisiones de objetos que rebotan sin perder energía.

Introducción:

Cuando uno piensa en π, lo primero que se viene a la cabeza es un círculo. Quizás alguna fórmula del colegio, con telarañas, como: circunferencia=2πr. O quizás, si eres más viejito, 3.14 y ya.

Pero lo que probablemente no te imaginas es que π también puede aparecer en una pista de autitos chocadores. Nada de compases, ni medir radios ni usar reglas raras. Solo dos “autitos” (en realidad bloques de masa m, pero la idea se entiende), una muralla, y varios porrazos.

Y lo más loco: la cantidad total de choques te da los primeros dígitos de π.

Un poco (¡poquito!) de Historia.

La idea de que hay una relación constante entre el diámetro y el perímetro de un círculo es muy antigua.

Los babilonios, hace unos 4.000 años, ya usaban una aproximación de π ≈ 3,125.
Los egipcios, según el papiro Rhind (alrededor del 1650 a.C.), tenían su propia fórmula que daba un valor cercano a 3,1605.

Pero el más seco fue Arquímedes, en la antigua Grecia (siglo III a.C.). Sin calculadora, sin álgebra, y solo con geometría, logró estimar π entre 223/71 (3,1408) y 22/7 (3,1429). ¿Su método? Usar polígonos para encerrar el círculo y calcular perímetros desde adentro y desde afuera. Un verdadero capo.

Durante siglos, π fue un número que se calculaba a partir de curvas y círculos. Y luego, de pronto, aparece escondido entre rebotes.

El Experimento:

Imagina una pista completamente lisa, sin fricción. A un lado, una muralla. Sobre la pista, dos bloques (o autitos, si prefieres mantener el juego):

• Uno más liviano, cerca de la muralla.
• Otro más pesado, más lejos, moviéndose hacia el primero.

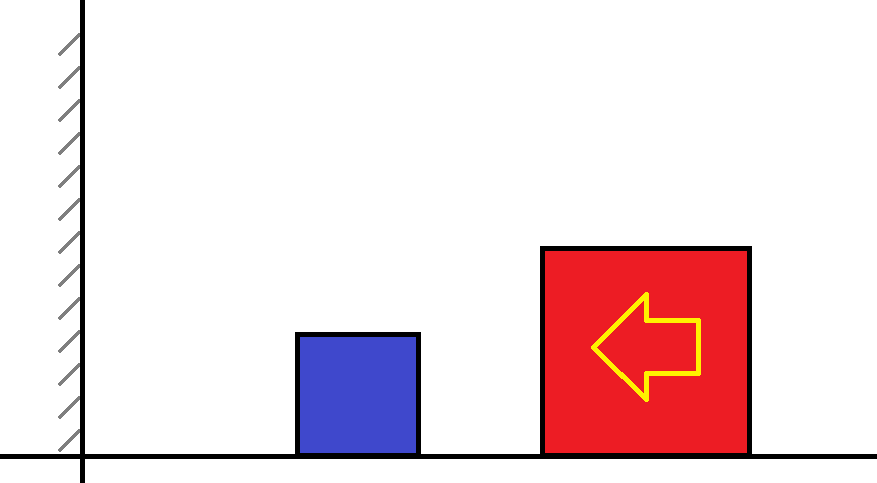
Ambos se deslizan suavemente. Cada vez que chocan entre sí o con la muralla, lo hacen de forma perfectamente elástica: No pierden velocidad, no se aplastan, solo rebotan.

Si el bloque más grande tiene 100 veces más masa que el pequeño, se producen 31 choques antes de que ambos salgan disparados hacia la derecha.

Si la masa del bloque grande es 10.000 veces mayor → 314 choques
Si es 1.000.000 veces → 3.141 choques
Y así, agregando ceros, aparecen más y más dígitos de π. Todo esto, sin tocar un compás. Esto es elegantemente explicado en el siguiente video de @3blue1brown:

Esto no es magia: es matemática

Aunque parezca un truco de feria o una casualidad simpática, todo esto está respaldado por matemática pura. En el año 2003, el matemático ruso G. Galperin publicó un artículo donde demostró formalmente que el número total de choques en este sistema está directamente relacionado con los dígitos de π.
El trabajo se llama “Playing pool with π (the number π from a billiard point of view)”, y fue publicado en la revista Regular and Chaotic Dynamics. Puedes leerlo aquí.

El sistema está gobernado por dos principios de la mecánica clásica:

1. Conservación de la cantidad de movimiento (momentum):

En ausencia de fuerzas externas, la cantidad total de movimiento antes y después de cada choque se conserva:

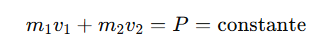
2. Conservación de la energía cinética :

Dado que los choques son perfectamente elásticos:

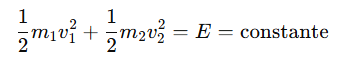
Estas dos ecuaciones permiten determinar las velocidades después de cada choque entre los bloques. Tras hacer una normalización podemos y definir variables x e y útiles,

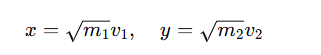
veremos que la conservación de energía se convierte en restricciones de estar dentro de un circulo:

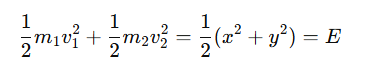
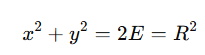
y la de momento, seguir una recta, dentro de un espacio de estados definidos por las velocidades:

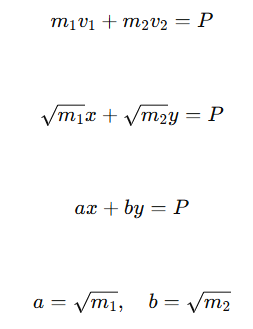
Esto lo explica mucho mejor 3Blue1Brown en el siguiente video:

Simulemos:

def choque_elastico(v1, v2, m1, m2):
    """Calcula las velocidades después de un choque elástico unidimensional."""
    v1_final = ((m1 - m2) * v1 + 2 * m2 * v2) / (m1 + m2)
    v2_final = ((m2 - m1) * v2 + 2 * m1 * v1) / (m1 + m2)
    return v1_final, v2_final

def simular_choques(m1, m2):
    v1 = 0.0    # bloque pequeño empieza quieto
    v2 = -1.0   # bloque grande se mueve hacia el bloque pequeño (hacia la izquierda)
    choques = 0

    while True:
        # choque entre bloques
        v1, v2 = choque_elastico(v1, v2, m1, m2)
        choques += 1

        # choque con pared del bloque pequeño
        if v1 < 0:
            v1 = -v1
            choques += 1
        else:
            # si el bloque pequeño ya no va hacia la pared y el bloque grande va alejándose, terminamos
            if v2 > v1:
                break

    return choques

if __name__ == "__main__":
    masas = [1, 100, 10_000, 1_000_000]
    for m2 in masas[1:]:
        m1 = 1
        choques = simular_choques(m1, m2)
        print(f"Con masa bloque pesado = {m2}, choques totales = {choques}, π aproximado = {choques / 10**(len(str(m2))-1)}")

Al correr obtenemos:

Con masa bloque pesado = 100, choques totales = 31, π aproximado = 0.31
Con masa bloque pesado = 10000, choques totales = 314, π aproximado = 0.0314
Con masa bloque pesado = 1000000, choques totales = 3141, π aproximado = 0.003141

Epilogo

Calcular pi con choques elásticos es, desde una perspectiva computacional, ineficiente y altamente impráctico. A medida que se buscan más cifras, la simulación requiere una precisión temporal cada vez mayor y se vuelve casi imposible de ejecutar en tiempo real. Lo fascinante es que este modelo, basado únicamente en la conservación de energía y cantidad de movimiento, no solo funciona, sino que también guarda conexiones profundas con ideas de la mecánica cuántica, los sistemas hamiltonianos y el cómputo reversible.

Y sin embargo, hay algo valioso en este tipo de experimentos. Tal como cuando alguna vez intentamos capturar todos los Pokémon —una tarea absurda en apariencia, sin una meta clara—, a veces el primer paso para crear una herramienta útil o resolver un problema es justamente lanzarse a lo aparentemente inútil. Lo importante no es completar la tarea, sino lo que aprendimos intentándolo.